JCMoptimizer

JCMoptimizer comprises many tools for the efficient analysis and optimization of physical systems and numerical functions that are expensive to evaluate. We have a free tier, so you can easily try it out. Read the installation guide for Python or Matlab or - to get started quickly - just follow these 3 steps:

  1. Install our python package: pip install jcmoptimizer.
  2. Create an API access token.
  3. Optimize your first function:
from jcmoptimizer import Client, Study, Observation
from my_module import expensive_evaluation
client = Client(token=...)

study = client.create_study(
    design_space= [
        {'name': 'x1', 'type': 'continuous', 'domain': (-1,1)}, 
        {'name': 'x2', 'type': 'continuous', 'domain': (-5,5)},
    ],
    driver="BayesianOptimization",
)

def evaluate(study: Study, x1: float, x2: float) -> Observation:
    value = expensive_evaluation(x1, x2)
    observation = study.new_observation()
    observation.add(value)
    return observation

study.set_evaluator(evaluate)
study.configure(max_iter=500, num_parallel=5)
study.run()
print(f"Minimum at {study.driver.best_sample}")

Applications - Black Boxes Everywhere

Science an engineering is full of black box systems whose behavior is not perfectly predictable without an elaborate execution - for example a time consuming CFD simulation or an energy consuming physical experiment. JCMoptimizer has been developed to predict, understand and optimize the outcome of those systems.

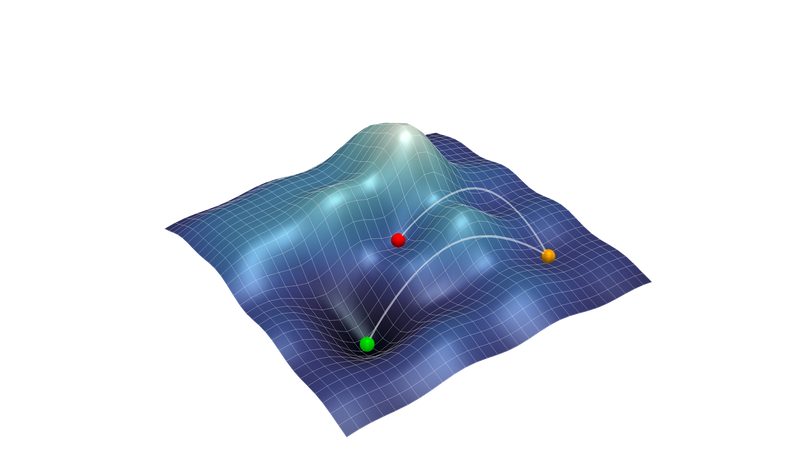
Optimization

The global minimization of a function that depends on many parameters is a challenging problem. While traditional methods, like swarm based of evolutionary algorithms, rely on heuristic trial and error principles, Bayesian Optimization uses stochastic machine learning models to steer a much more informed search for the minimum. Bayesian optimization hence escapes local minima and has typically a ten times shorter run time.

Read more:

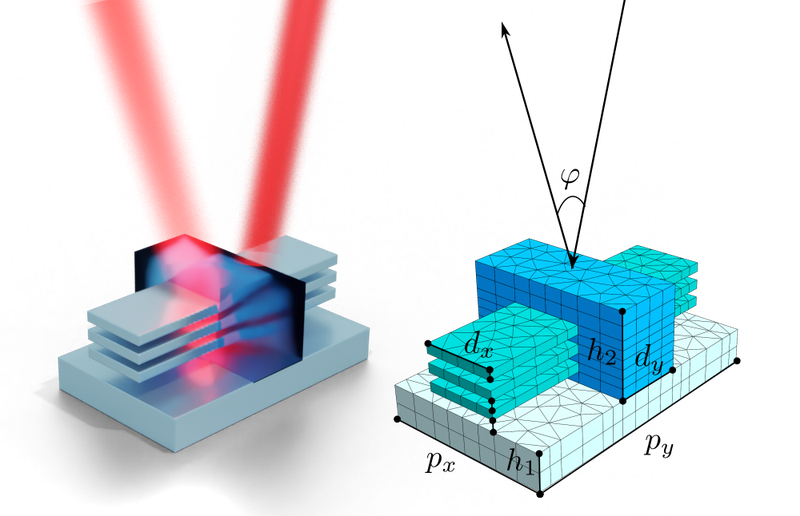
Model Calibration

Digital twins are a powerful tool to understand and control physical systems. However, it is often impossible to build models from first principles and some parameters of the models remain unknown. On can use measurements of the physical system to calibrate the model. If the numerical model requires the solution of differential equations, this calibration can be very time consuming. JCMoptimizer provides tools to reconstruct the parameters from measurements extremely efficiently. It can also determine the full probability distribution of model parameters using Markov chain Monte Carlo (MCMC) sampling. This makes it ideal in the context of inverse measurements, such as scatterometry.

Read more:

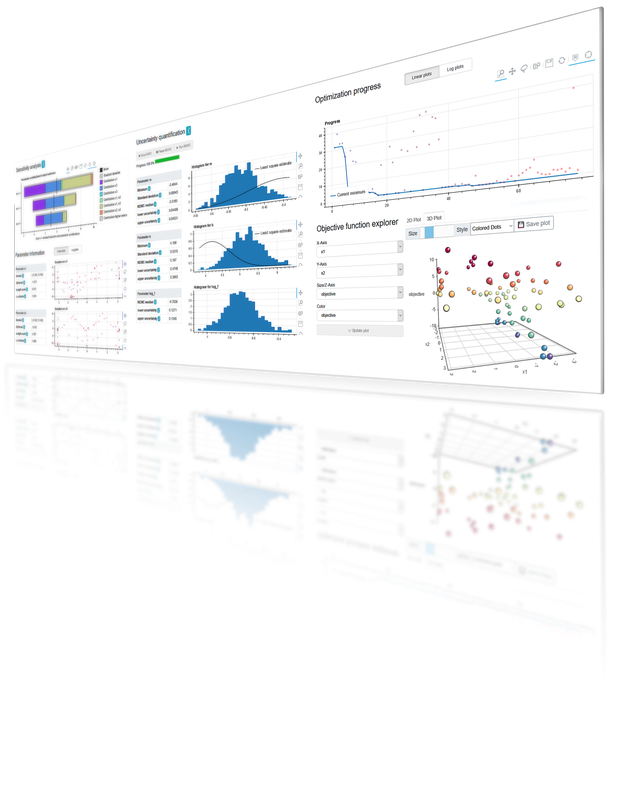
Multi Objective Optimization, Active Learning, Sensitivity Analysis, and More

JCMoptimizer's offers a very flexible architecture that enables many different applications, such a multi objective optimization, the active training of a global surrogate, or a global sensitivity analysis in terms of Sobol' coefficients. To learn more, have a look at our tutorials:

Technology and Tools

JCMoptimizer is based on many years of research and technology development on the field of optimization and machine learning.

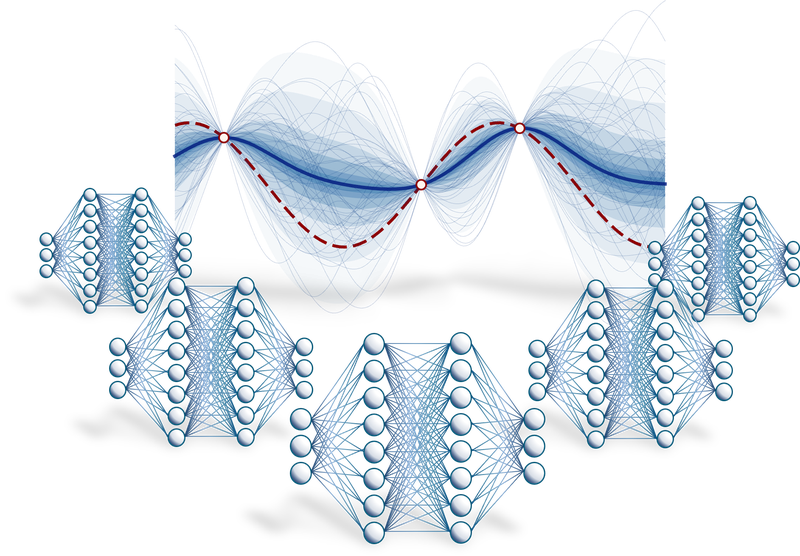
Machine Learning

We use machine learning models - neural network ensembles or Gaussian processes - that are able to make probabilistic predictions from very few observations. These models drive a highly efficient study of the system with the goal to optimize one or more outcomes, fulfill constraints, or maximize prediction accuracy.

Read more:

Flexible Configuration

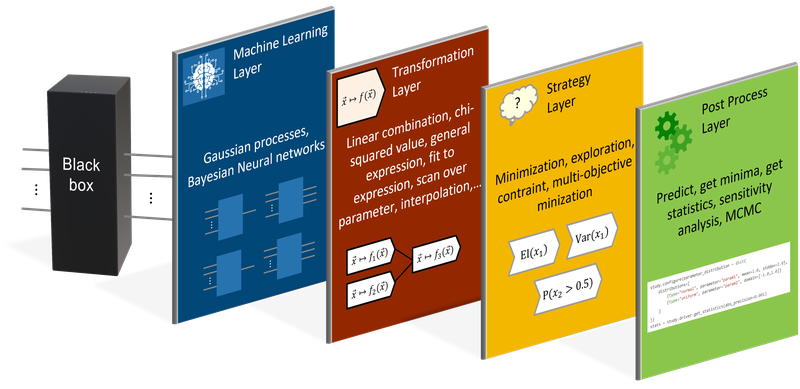
JCMoptimizer allows to configure multiple processing layers in order to define almost arbitrary machine learning-based studies:

  • In the Machine Learning Layer on can define one or more surrogate models (Gaussian processes, neural network ensembles) that learn scalar or vectorial functions.
  • In the Transformation Layer the stochastic predictions of the surrogate can be combined and transformed to new stochastic variables.
  • In the Strategy Layer the stochastic variables can be defined to drive the sampling strategy of the study.
  • The Post Process Layer enables additional analysis of the trained model.

Read more:

Powerful Interfaces

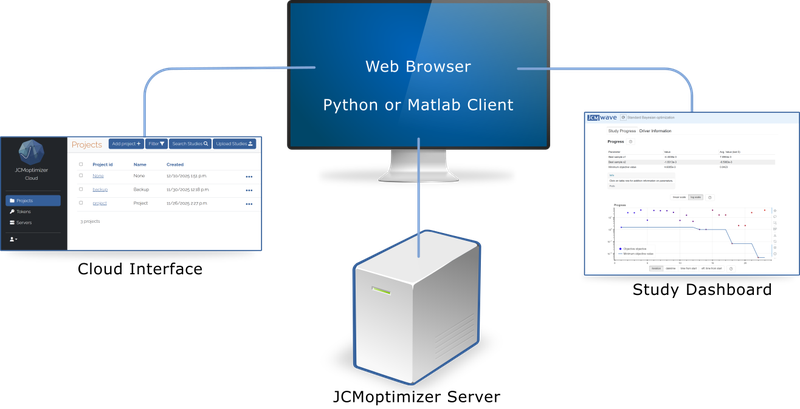
JCMoptimizer is combined of multiple browser based and scripting based interfaces.

Cloud Interface

In the JCMoptimizer Cloud interface one can manage studies that are organized into projects. One can also start new JCMoptimizer servers and create tokens to access the cloud infrastructure.

Study Dashboard

When a study is run through the Python or Matlab clients, its progress can be observed on the study dashboard, which can be opened in any web browser.

JCMoptimizer Server

The JCMoptimizer server provides all functionalities to run a study. For example, it computes new suggestions to be evaluated or runs postprocesses based on the machine learning models trained during the study. One connects to the server via Python or Matlab clients :

The cloud infrastructure provides the most convenient way to use JCMoptimizer. However, you can also install the JCMoptimizer server on a local computer.

Research

We regularly cooperate with other research partners and publish important technological insights from our work on JCMoptimizer.